AtCoder Beginner Contest 442

RookieSama_

公告

欢迎来到小破站ようこそ私のブログへ！

Learn Morea

标签

2648 字

13 分钟

AtCoder Beginner Contest 442

2026-01-25

题解

ABC

/

linker-include

C - Peer Review #

题目大意：#

每个人都会发表文章，现在要选除了自己外的三个审稿人，问你最多有多少种选择
审稿人：必须与发表文章的人没有矛盾

输入:

输出:

1
0 1 0 4 4 10

理解和思路:#

因为审稿人必须与发表文章的人没有矛盾，因为数据提供的是矛盾，那我们就存储，每个人与其他人矛盾的数量, $n - a_i - 1$ 就是每个人能分配到的审稿人数
$C_{n-a_i-1}^{3}$ 就是每个人的答案其中 $a_i$ 表示第 i 个人的矛盾人数

代码:#

1
#include <bits/stdc++.h>
2
using namespace std;
3

4
#define IOS ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
5
const int N = 2e5 + 10;
6
#define int long long
7

8
int n, m;
9
int a[N];
10

11

12
int C(int n){
13
    return n * (n - 1) / 2 * (n - 2) / 3;
14
}
15

16
/**
17
 * @brief 计算每个顶点不参与的三元组数量
18
 * @details
19
 * 问题：给定无向图，对于每个顶点i，计算有多少个三元组(j,k,l)满足：
20
 * - j, k, l 互不相同
21
 * - j, k, l 都不与顶点i直接相连
22
 *
23
 * 算法思路：
24
 * 1. 统计每个顶点的度数a[i]（直接邻居数量）
25
 * 2. 对于顶点i，非邻居顶点数为：n - a[i] - 1（排除自己和直接邻居）
26
 * 3. 从这些非邻居中选3个顶点的组合数即为答案
27
 *
28
 * 组合数公式：C(n,3) = n*(n-1)*(n-2)/6
29
 *
30
 * 关键洞察：利用补集思想，计算"不参与"的三元组比直接计算"参与"的三元组更简单
31
 */
32
void solve(){
33
    cin >> n >> m;                    // 读取顶点数n和边数m
34

35
    // 步骤1：统计每个顶点的度数（邻居数量）
36
    // a[i]表示顶点i的直接邻居数
37
    for(int i = 1; i <= m; i++) {
38
        int x, y;
39
        cin >> x >> y;
40
        a[x]++, a[y]++;               // 无向图：两个顶点的度数都增加
41
    }
42

43
    // 步骤2-3：计算每个顶点的答案
44
    // 对于顶点i：非邻居数 = n - a[i] - 1，然后计算C(非邻居数, 3)
45
    for(int i = 1; i <= n; i++){
46
        int non_neighbors = n - a[i] - 1;  // 与顶点i不相连的顶点数
47
        cout << C(non_neighbors) << " ";   // 从这些顶点中选3个的组合数
48
    }
49
}
50

51
signed main(){
52
    IOS;
53
    int _ = 1;
54
    //cin >> _;
55
    while(_--){
56
        solve();
57
    }
58
}

D - Swap and Range Sum #

题目大意:#

给你一个队列，可以采取两个操作:
- 1. 交换 $a_x 和 a_{x+1}$
- 1. 计算 $a_l , a_r$ 之和

理解和思路:#

这题是区间和区间修改的板子题，可以采取多种方法:
- 1. 树状数组(简单快)
- 1. 线段树 (复杂慢)
这里采用树状数组解决

代码:#

1
#include <bits/stdc++.h>
2
using namespace std;
3

4
#define IOS ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
5
const int N = 2e5 + 10;
6

7
int n, m;
8
int a[N];
9
int tr[N];
10

11
void add(int x,int v){
12
    for(int i = x; i <= n; i += i & -i) tr[i] += v;
13
}
14

15
int sum(int x){
16
    int res = 0;
17
    for(int i = x; i ; i -= i & -i) res += tr[i];
18
    return res;
19
}
20

21
/**
22
 * @brief 动态数组区间查询 - 树状数组实现
23
 * @details
24
 * 问题：维护一个数组，支持两种操作：
25
 * 1. 交换相邻元素 a[x] 和 a[x+1]
26
 * 2. 查询区间 [x,y] 的元素和
27
 *
28
 * 算法：使用树状数组(Fenwick Tree)高效处理动态更新和区间查询
29
 *
30
 * 树状数组特点：
31
 * - 单点更新：O(log n)
32
 * - 前缀查询：O(log n)
33
 * - 空间：O(n)
34
 */
35
void solve(){
36
    cin >> n >> m;  // 读取数组长度n和操作数m
37

38
    // 初始化：读取数组并构建树状数组
39
    for(int i = 1; i <= n; i++) {
40
        cin >> a[i];      // 读取初始数组元素
41
        add(i, a[i]);     // 将元素添加到树状数组
42
    }
43

44
    // 处理m个操作
45
    while(m--){
46
        int op, x, y;
47
        cin >> op >> x;
48

49
        if(op == 1){
50
            // 操作1：交换相邻元素 a[x] 和 a[x+1]
51
            // 步骤：先从树状数组中移除旧值
52
            add(x, -a[x]), add(x + 1, -a[x + 1]);
53

54
            // 添加交换后的新值
55
            add(x, a[x + 1]), add(x + 1, a[x]);
56

57
            // 实际交换数组元素
58
            swap(a[x], a[x + 1]);
59
        }else{
60
            // 操作2：查询区间 [x,y] 的和
61
            cin >> y;
62
            // 利用前缀和性质：sum[y] - sum[x-1] = sum[x,y]
63
            cout << sum(y) - sum(x - 1) << endl;
64
        }
65
    }
66
}
67

68
int main(){
69
    IOS;
70
    int _ = 1;
71
    //cin >> _;
72
    while(_--){
73
        solve();
74
    }
75
}

E - Laser Takahashi #

题目大意：#

给你 N 个点在坐标轴上, 现在你可以 电眼逼人，站在原点向一个方向射线，可以串起在同一条直线的所有点，现在问你从 a 点到 b 点（顺时针转）总共射穿多少个点。

理解和思路:#

很明显本题需要我们找到一种快速计算 a - b间的所有点数量(包含a b同线上的所有点)
这就得考虑如何离散，如何排序，如何映射
- 1. 因为点本就是离散点，按照它给的顺序即可
- 1. 排序：因为要求顺时针转动，因此我们得为每一个点进行标号，从x正半轴顺时针旋转 360° ，的顺序进行标号
```
1
/*
2
(想要看懂 就画图 别光看)
3
比如给出: (1, 1) (1, -1) (-1, -1) (-1, 1)
4
表示原索引:  1      2        3        4
5
排序后：   (1, -1) (-1, -1) (-1, 1) (1, 1) 就是我们要的顺序
6
现在    2       3       4       1
7
对应的就是我们排序后的原始索引 (可以理解为哪个怪物被排到的编号1 - n)
8
*/
9
sort(ord + 1, ord + 1 + n, cmp);//排序
```
- 1. 映射: 我们排序完所得到的是 编号 i 的原始索引，给我买查询的值是原始索引，我们得反向映射到排序后的结果, 即是原始索引所在的排序位置

1
    for(int i = 1; i <= n; i++)
2
        rev[ord[i]] = i; // 记录原始索引在排序中的位置

排序和映射可以通俗的理解为: - 在坐标系图中排序为第 i 个怪兽是编号为 j 的怪兽 - 同时编号为 j 的怪兽在坐标系中排序为第 i 个怪兽
那如何排序呢
- 首先，确定每个点 (x,y) 属于哪个半平面。
  - 上半平面： y>0 或( y=0 和 x>0 )。
  - 下半平面：反之
- 这个标准可以区分参数是属于 [0,180°) 还是 [180°,360°) ，作为参数的粗略排序。
- 请看下面这个图(叉乘)
- 令 $\vec{a}=(x_1,y_1),\vec{b} =(x_2,y_2)$
- 则 $\vec{a} \times \vec{b} == x_1*y_2 - x_2*y_1$ 通过下面的图我们就可以发现:
- $\vec{a} \times \vec{b} <0$ 则说明 a 顺时针旋转到 b 反之逆时针
- 我们先按照从 x 正半轴逆时针的排序(这样可以让 0° 和 360°重合)
- 此时我们就得到一个排序完的原始索引
- 由于我们得到的序列是逆时针,题目要求顺时针，就反转一下 reverse()
得到排序后的原始索引需要再被反向映射用于查找:
- 我们映射反向索引即可

向量图

1
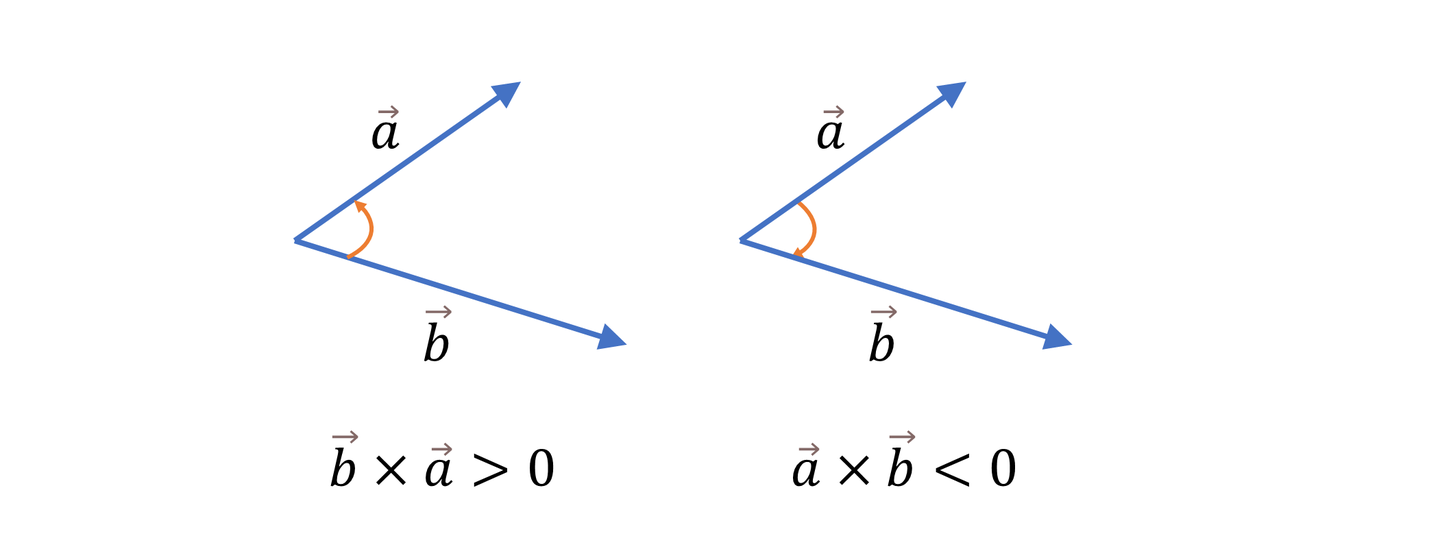
  //给出我们的cmp
2
  int col(Point a, Point b){ //计算叉乘
3
    return a.x * b.y - a.y * b.x;
4
}
5
bool cmp(int a, int b){ // 让y轴正半轴上的点优先排序 并且是逆时针排序
6
    Point pa = pt[a], pb = pt[b]; //获取a,b的坐标
7
    int ha = (pa.y < 0 || (pa.y == 0 && pa.x < 0)); // ha < 0 表示在y的正半轴
8
    int hb = (pb.y < 0 || (pb.y == 0 && pb.x < 0)); // ha > 0 表示在y的负半轴
9
    if(ha != hb) return ha < hb; // 判断是否在同一y半轴上 优先排 y 正半轴上的点
10
    return col(pa,pb) > 0; // 计算叉乘 大于0 表示pa在pb的逆时针方向
11
}

最后统计在编号为 $l,r$ $l, r$ 之间的所有点数量即可
- 我们用前缀和预处理，快速计算 $[l,r]$ 之间的怪兽数量
- $l[i]$ 表示从编号 0 到编号 i 中间所有的怪兽的数不包含编号 i 以及编号共线的所有点 (切记从前往后)
- $r[i]$ 表示从编号 0 到编号 i 中间所有怪兽的数量包含编号 i 以及编号共线所有点 (切记从后往前)
- ```
1
    l[1] = 0, r[n] = n;
```

// 初始化 l 和 r for(int i = 2; i <= n; i++) l[i] = (cmp(ord[i], ord[i - 1])) ? i - 1: l[i - 1]; //不包含 i 点 for(int i = n - 1; i >= 1; i—) r[i] = (cmp(ord[i + 1], ord[i])) ? i : r[i + 1]; // 包含 i 点 ``` - 当编号 $a < b$ 时 : $r[b] - l[a]$ - 当编号 $a > b$ 时: $N - l[a] + r[b]$

代码：#

1
#include <bits/stdc++.h>
2
using namespace std;
3

4
#define int long long
5
#define IOS ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
6
const int N = 2e5 + 10;
7
using PII = pair<int,int>;
8
int n, m;
9
int ord[N];// 存储按照特定顺序排列的原始索引
10
int rev[N];// 反向映射 存储原始索引在排序中的位置
11
// l[i] 表示从原始点到 i 顺时针方向所经过的所有点的总数(但不包括在同一轴上的所有点)
12
// r[i] 同理， 但包含 i 点
13
int l[N], r[N];
14
class Point{
15
public:
16
    int x, y;
17
};
18

19
Point pt[N]; //记录N个怪物
20

21
int col(Point a, Point b){ //计算叉乘
22
    return a.x * b.y - a.y * b.x;
23
}
24

25
bool cmp(int a, int b){ // 让y轴正半轴上的点优先排序 并且是逆时针排序
26
    Point pa = pt[a], pb = pt[b]; //获取a,b的坐标
27
    int ha = (pa.y < 0 || (pa.y == 0 && pa.x < 0)); // ha < 0 表示在y的正半轴
28
    int hb = (pb.y < 0 || (pb.y == 0 && pb.x < 0)); // ha > 0 表示在y的负半轴
29
    if(ha != hb) return ha < hb; // 判断是否在同一y半轴上 优先排 y 正半轴上的点
30
    return col(pa,pb) > 0; // 计算叉乘 大于0 表示pa在pb的逆时针方向
31
}
32

33
void solve(){
34
    cin >> n >> m;
35
    for(int i = 1; i <= n; i++){
36
        cin >> pt[i].x >> pt[i].y;
37
    }
38
    // 按照cmp的规则排序 大概是 0-90-180-270-0° 从第一象限开始逆时针排序
39
    for(int i = 1; i <= n; i++) ord[i] = i;
40
    sort(ord + 1, ord + 1 + n, cmp);
41
    reverse(ord + 1, ord + 1 + n); //反转 变成 0-270-180-90-0° 从第四象限开始顺时针排序
42

43
    for(int i = 1; i <= n; i++)
44
        rev[ord[i]] = i; // 记录原始索引在排序中的位置
45

46
    l[1] = 0, r[n] = n;
47
    // 初始化 l 和 r
48
    for(int i = 2; i <= n; i++)
49
        l[i] = (cmp(ord[i], ord[i - 1])) ? i - 1: l[i - 1]; //不包含 i 点
50
    for(int i = n - 1; i >= 1; i--)
51
        r[i] = (cmp(ord[i + 1], ord[i])) ? i : r[i + 1]; // 包含 i 点
52

53
    while(m--){
54
        int a, b;
55
        cin >> a >> b;
56
        a = l[rev[a]];
57
        b = r[rev[b]];
58
        if(a < b) cout << b - a << endl;
59
        else cout << n - a + b << endl;
60
    }
61
}
62

63
signed main(){
64
    IOS;
65
    int _ = 1;
66
    //cin >> _;
67
    while(_--){
68
        solve();
69
    }
70
}

本题收获：#

本题是我

AtCoder Beginner Contest 442

https://blog.rookiesama.space/posts/atcoder/atcoder-beginner-contest-442/

作者

Rookiesama

发布于

2026-01-25

许可协议

CC BY

部分信息可能已经过时

Easy Glide

Codeforces Round 1075 (Div. 2)

素晴らしき日々

C - Peer Review#

题目大意：#

理解和思路:#

代码:#

D - Swap and Range Sum#

题目大意:#

理解和思路:#

代码:#

E - Laser Takahashi#

题目大意：#

理解和思路:#

代码：#

本题收获：#

C - Peer Review #

D - Swap and Range Sum #

E - Laser Takahashi #